Hé oui rien que ça… Je tiens à préciser que même si vous ne comprenez pas un mot au langage mathématique cet article est pour vous ! Pour commencer demandons-nous ce que ça signifie. Les nombres Réels ? Ils doivent donc exister. C’est un bon début. Ce sont des nombres qui existent concrètement (à noter que la notion d’existence d’un nombre est assez relative puisqu’un nombre n’est qu’un concept créé de toute pièce par les Humains). L’ensemble des réels c’est donc un gros paquet de nombres qui existent. Mais finalement, qu’est-ce qu’il y a dans cet ensemble. Et surtout pourquoi n’arrêtent-t-on pas d’en entendre parler de la seconde à la terminale ? C’est ce que je vais tenter de vous expliquer dans cet article.
L’ensemble des nombres Réels c’est bien gentil, mais c’est quoi un ensemble ?
En mathématiques, comme dans la vie, un ensemble est une collection d’objets. Par contre, en mathématiques, on a absolument pas peur de construire une collection contenant un nombre infini d’objets. Ici bien sur on parle d’objets mathématiques. Ces objets, ce sont des nombres. Des concepts imaginés par les humains pour représenter une certaine quantité. Un ensemble c’est donc comme un grand sac mental, dans le quel on peut mettre ce que l’on veut, y compris des sac plus petits ! En effet un ensemble peut tout à fait en contenir un autre et ce sera tout le propos de cet article. Nous allons en effet commencer par le plus petit sac contenu dans l’ensemble des réels.
Les nombres Entiers Naturels
Ce sont les nombres avec lesquels nous sommes les plus familiarisés. Si je vous demande maintenant de penser à un nombre tout de suite sans réfléchir… Normalement vous devriez avoir 1 ou 2 ou 3 en tête, peut-être 42 pour les plus tordus ! Bref vous venez de penser à un nombre sans virgule et positif. Hé bien c’est cela les entiers naturels. Tous les nombres 0, 1, 2, 3… etc jusqu’à l’infini. Voilà votre premier sac mental dont le symbole est un grand N. Par exemple on dira que le nombre 17 appartient aux entier naturels ce qui en langage mathématique donne: 17 ∈ N
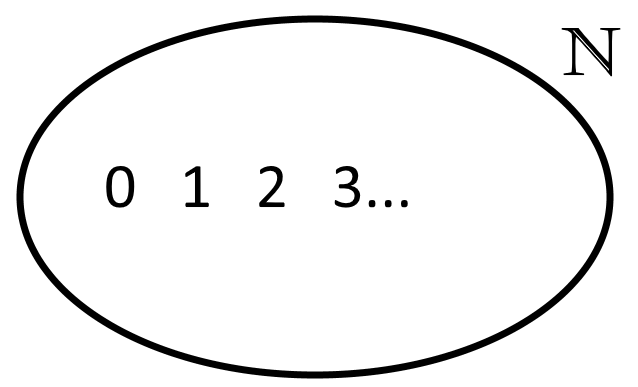
Mais vous vous en doutez, les entiers naturels ne sont pas suffisants. Comment exprimer une quantité, mais en moins ? Quelque chose que l’on retire ou de l’argent que l’on doit ? C’est là qu’intervient le sac suivant…
Les Nombres Entiers Relatifs
L’ensemble des entiers relatif n’est qu’une extension des entier naturels auquel on ajoute tous les entiers négatifs. Une sorte d’image miroir des entiers naturels que l’on ajoute à ces derniers. Ces nombres tels que -1, -2 etc sont les “opposés” de leur collègues positifs. Deux nombres opposés ont la particularité de s’annuler si on les ajoute. Ce nouvel ensemble a pour symbole un grand Z. Pour remplir ce sac on met donc le sac précédent ( les entiers naturels ) plus les entiers négatifs. Et voilà ce que l’on obtient:
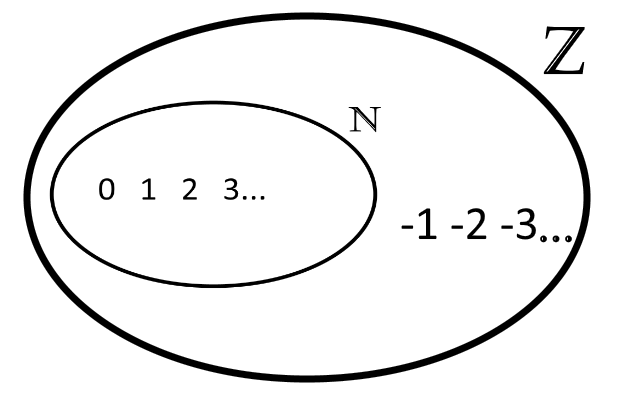
Maintenant un nouveau problème se pose à nous. Comment faire pour exprimer une quantité qui ne soit pas entière ? Comment écrire de façon simple 1 kilogramme plus la moitié d’un kilogramme ? C’est ici qu’intervient l’ensemble suivant.
Les nombres décimaux
Les nombres décimaux, comme leur nom l’indique, sont des nombres comportant des décimales. Ces décimales (chiffres après la virgule) permettent de situer une quantité entre deux quantités exprimées par des entiers. Les nombres décimaux comprennent donc tous les nombres vus précédemment ainsi que tous les nombres que l’on peut construire en ajoutant des décimales à ces derniers. Cet ensemble à pour symbole un grand D.
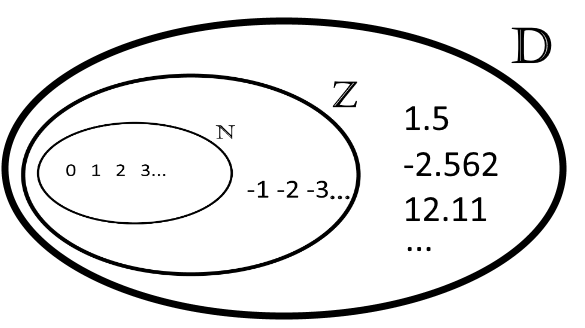
Nous voilà donc avec un ensemble de nombres, positifs ou négatifs. Sans décimales ou avec un certains nombre de décimales. J’insiste sur le fait que le nombre de décimales d’un nombre décimal doit être connu. Pour faire simple, si vous avez un papier assez grand et assez de temps devant vous, vous devez pouvoir écrire un nombre décimal dans sa totalité.
Toutefois cela nous amène un nouveau problème. Que se passe-t-il si vous divisez 1 par 3 ? Si vous savez poser une division ou si vous avez une calculatrice sous la main, vous obtiendrez 0,3333333333… Cela ne s’arrête jamais. Vous voyez ou je veux en venir ? Peu importe la taille de votre feuille et le temps que vous avez devant vous, il est impossible d’écrire ce nombre en entier. 1⁄3 ne fait donc pas parti de l’ensemble des décimaux.
Les Nombres rationnels
Contrairement aux nombres décimaux, les nombres rationnels ne sont pas limités par le nombre de leurs décimales. Un nombre comme 1⁄3 ou même 13⁄7 sont des nombres rationnels. Leurs décimales s’étendent à l’infini. Parfois le même chiffre se répète comme dans 1⁄3 (0,3333333333…). Il arrive que la même série de chiffres soit reproduite à l’infini comme dans 13⁄7 (1,857142857142857142857142857…). Mais tous les nombres de l’ensemble des Rationnels un point commun : on peut toujours les écrire sous la forme d’une fraction de deux entiers. Et cela se vérifie avec les nombres de tous les ensembles précédents. En effet 1 peut s’écrire sous la forme d’une fraction 1⁄1 comme tous les autres entiers, -2 = -2⁄1. Il en est de même pour les décimaux. N’importe quel décimal comme 1,457896 peut s’écrire sous la forme d’une fraction 1,457896 = 1457896⁄1000000. On peut donc mettre tous les ensembles précédents à l’intérieur de celui-ci. Les nombres rationnels sont symbolisés par la lettre Q.
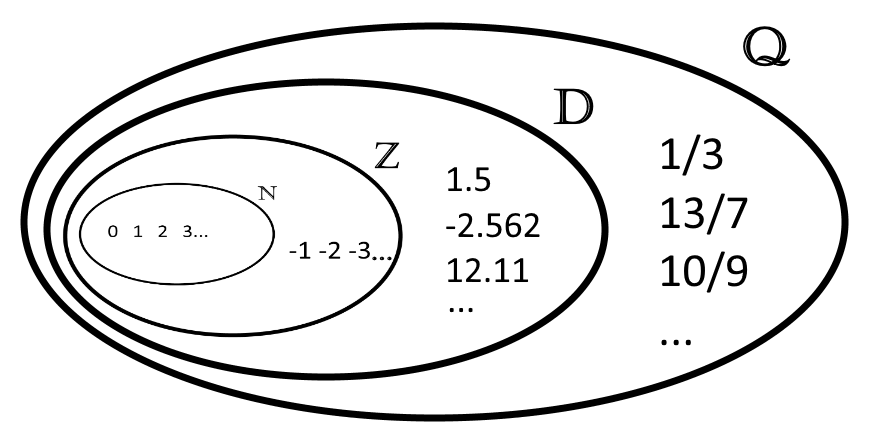
Dès lors, on pourrait penser que nous avons parcouru tous les nombres : positifs, négatifs, entiers, à virgule, avec un nombre fini ou infini de décimales. Cependant, certains nous on encore échappé. Imaginez des nombres, avec des décimales à l’infini et des décimales qui ne respectent aucun schéma répétitif.
Les nombres Réels
En plus de tous les ensembles précédents, l’ensemble des réels inclue aussi les nombres dont les décimales ne s’arrêtent jamais et ne présentent aucune régularité. Ils sont assez difficile à imaginer et pourtant il en existe un très célèbre dont tout le monde a déjà entendu parler. Je parle bien sûr de “Pi” noté π. Pi représente le rapport entre la circonférence d’un cercle et son diamètre. Ce nombre vaut 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820… etc. À l’heure actuelle on connait environ 10 000 milliards de décimales de Pi. Et peu importe jusqu’où nous allons, pas de schéma régulier, rien de répétitif, chaque décimale semble avoir été tirée au hasard entre 0 et 9. Ainsi l’ensemble des réels contient tous les ensembles précédent auxquels il faut ajouter tous les nombres tel que π , racine carrée de 2, ou encore le nombre e. On obtient ainsi la représentation imbriquée de l’ensemble des réels dont le symbole est un R:
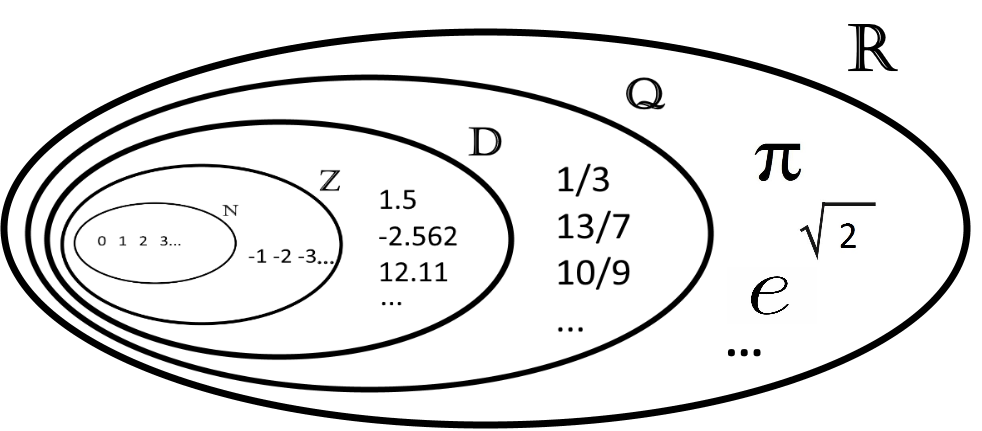Voilà les nombres principaux auxquels vous serez confronté dans la vie et en mathématiques. Toutefois l’ensemble des Réels n’est pas le plus grand ensemble. Il existe un sac bien plus grand encore que l’on nomme les nombres complexes mais ça c’est une autre histoire que seuls les élèves de terminale et les initiés connaissent. J’écrirai probablement un article sur ces nombres prochainement.
Il est important de savoir de quoi l’on parle
J’espère avoir clarifié les choses concernant ces ensembles. Et si en classe on vous oblige toujours à dire à quel ensemble appartiennent les nombres que vous manipulez ce n’est pas pour rien… En effet certaines équations n’ont de résultat que dans certains ensembles et pas dans d’autres. Certaines formules ne marche qu’avec des nombres appartenant à un ensemble bien précis. Par exemple on peut écrire tous les nombres pairs positifs de cette façon: 2k avec k ∈ N. Cela ne fonctionne plus si l’on écrit k ∈ R car dans cette formule k doit impérativement être un entier positif.
Souvenez vous de tout cela et quand vous verrez un R, un N, un Q ou n’importe quel autre ensemble, demandez vous toujours pourquoi l’on vous donne cette information et que cela implique-t-il pour votre exercice.
Sur ce je vous souhaite une agréable journée pleine nombres appartenant à l’ensemble de votre choix !
Mathématiquement,
-Ben-